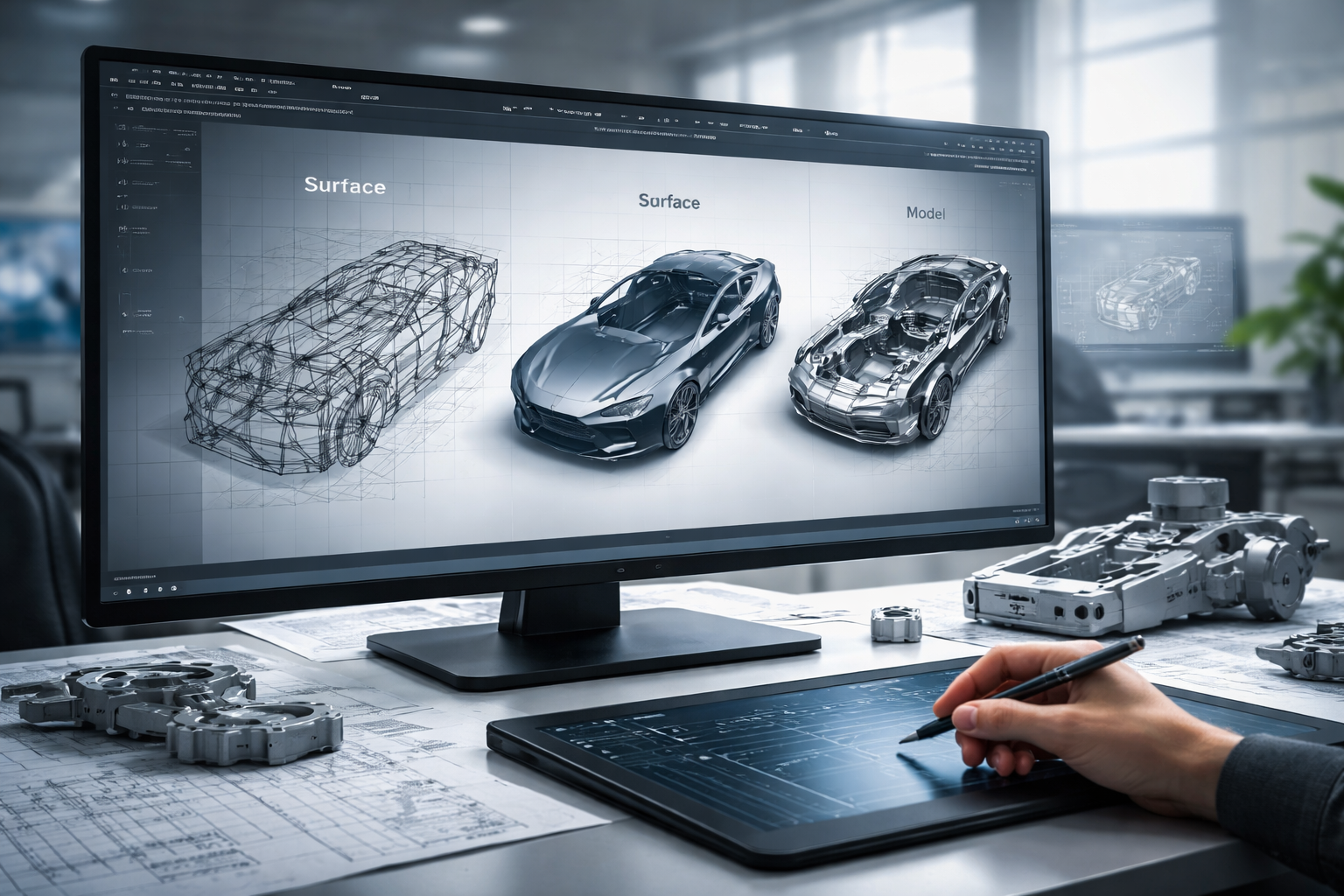
Geometric modeling is a significant technique in computer graphics and scientific visualization and engineering design. First of all it is not about merely drawing shapes on a screen it is about drawing complicated shapes and structures using the aid of precise mathematical structures. Geometric modeling has been used to compute the accurate and flexible representation of shapes by manipulating coordinate systems, vector algebra, transformations and parametric equations, to facilitate the use of shapes in CAD design, in virtual simulation.
To gain a more detailed insight into geometric modeling, the mathematical foundations of such representations will have to be looked into.
The Geometric Modeling of Understanding
Geometric modeling is a mathematical model of shapes, surfaces and volumes in a digital medium. Geometric models have precise numerical data and equations unlike the hand-drawn sketches which are purely visual. The mathematical operations that are done with this mathematical model are complex (rotation, scaling, and deformation) and provide the accuracy.
The biggest advantage of the geometric modeling is in the fact that it bridges the gap between mathematical theory and the actual technologies of visualization. Engineers, architects, and scientists use these mathematical structures in coming up with realistic simulation and design solutions, which would not have been created through hand-drafting.
The Representation Coordinate Geometry of Backbone of Shape Representation
Coordinate geometry or analytic geometry provides a system of locating the points in space in a fundamental way. In two dimension, a point is represented as a pair (x, y) (x, y)(x,y,z), and in three dimension it is represented as a three-tuple (x,y, z) (x,y,z). These are the coordinates on which lines, curves and surfaces are defined.
Points, Lines, and Planes
- Points: This is the simplest geometric object that is co-ordinated.
- Lines: A point and directional or a contact point of two planes characterize lines. The 3D line equation can be expressed as a parametric equation and it is:
r(t) = r0 +tv u r(t) = r = r0 + tvr(t) = r = r0 + tvr(t) = r0 + vkor(t) = r0 + tgtwr(t) = r0 + tghwr(t) = r0 + tghwr(t) = r0 + tghwr(t) = r0 + tghwr(t) = r0 + tghwr(t) = r0 + tghwr(t) = r0 + tghwr(t) = r0
r0r0r0 is a position vector at the origin of a trajectory, vv is the direction vector and ttt is a scalar parameter. - Planes: they are defined by a point, and a normal plane. The equation of a plane is:
ax+by+cz+d=0ax + by + cz + d = 0ax+by+cz+d=0
in which (a,b, c) (a, b, c) (a,b,c) is the normal, and ddd is the distance of origin.
Coordinate geometry makes possible the geometry model system, which entails location, manipulation and computation relationships between shapes within a geometric system. All other methods of modeling have a mathematical scaffolding that they are based on.
The Geometric Modeling of Vector Algebra
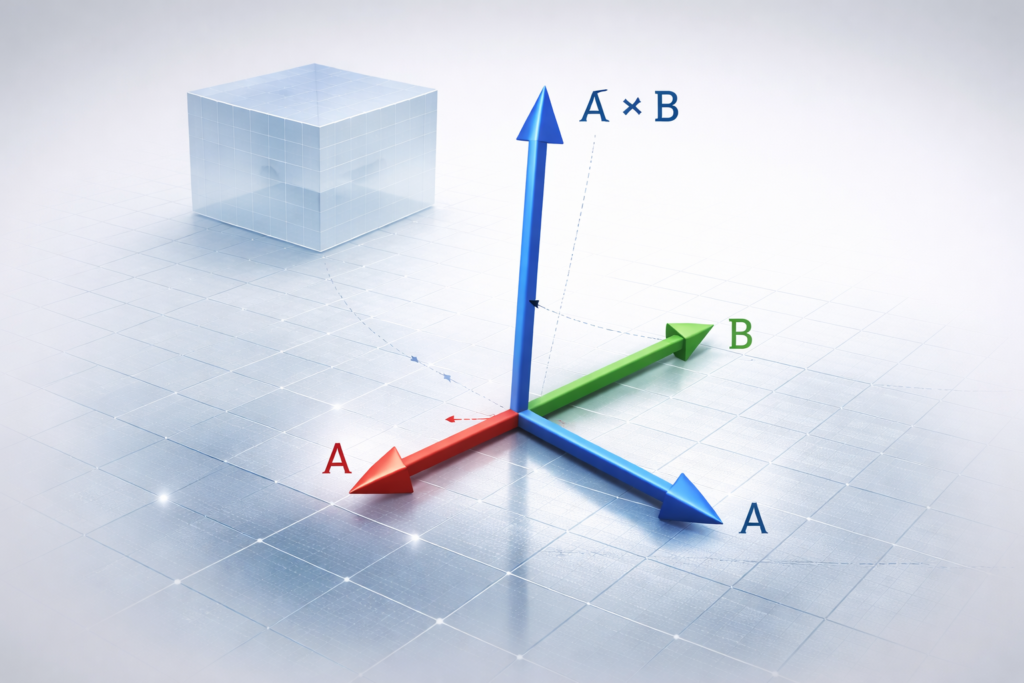
The introduction of the concept of the vector algebra has a broadening of the capabilities of the geometry of coordinates together with the equipping with the means of direction, magnitude, and space relations. Vectors play a significant role in modeling as they describe movement, the direction and magnification of things.
Key Vector Operations
- Adding and subtracting vectors: Addition and subtraction of vectors to obtain resultant positions.
- Scale Multiplication: Scale vector magnitude, required in scaling transformations.
- Dot Product (A[?]B\mathbf{A} -. …)
A[?]B=[?]A[?]BcoshthetaA[?]BA[?]B = A B cos theta. - Cross Product (AxB A times B A times B): Finds a normal (perpendicular) vector to two known vectors, which can be used to render surface normals in 3D graphics.
Geometric Modeling Application
The applications of vector algebra are rendering, computation of collision detection and shading. A case in point is surface normals computed by cross product that characterize the conduct of light on a three dimensional object that directly influences visualisation realism.
Transitions: Mobility and Change Models
Transformations Transformations are mathematical functions that move the position of geometric objects, their direction, or their size. They also play a central role in manipulation of models in computer graphics, animation and in CAD systems.
Types of Transformations
- Translation: Moves an object in one location to another without changing the shape or orientation of an object. Mathematically, P(x, y, z)P(x, y, z)P(x,y,z): T( tx,ty,tz):
P’=P+TP’ = P + \mathbf{T}P’=P+T - Scaling: This is the size of a given object which is enlarged or reduced but nothing is changed in terms of shape. In uniform scaling there is a single scaling factor as compared to non-uniform scaling which can have the ability to stretch objects in the direction desired.
P + (zsx,ysy,zsz)P + (x sx, y sy, z sz)P +(xsx,ysy,zsz) - Rotation: Rotations along a specific axis. Smooth interpolations of rotation can be expressed in three dimensions either in rotation matrices or quaternions. Z rotation using the angle, th thetath, is:
[x’y’z’]= -sin[?]th[?]cos[?]th0sin[?]thcos[?]th0001xyz - Reflection: This facilitates modelling of symmetry and is mirror to mirror to mirror.
- Shearing: Squeezes the shape along that particular axis, and this is useful in any particular style of art or industry.
Homogeneous Coordinates
In geometric modeling Geometric modeling Geometric modeling often uses homogeneous coordinates, which is an extra dimension on each point, to ensure that it is easy to perform combined transformations. This allows the case of translations, rotations and scalings representing themselves as multiplications of matrices, allowing one to chain a series of transformations together.
Parametric Equations: Curves and Surfaces
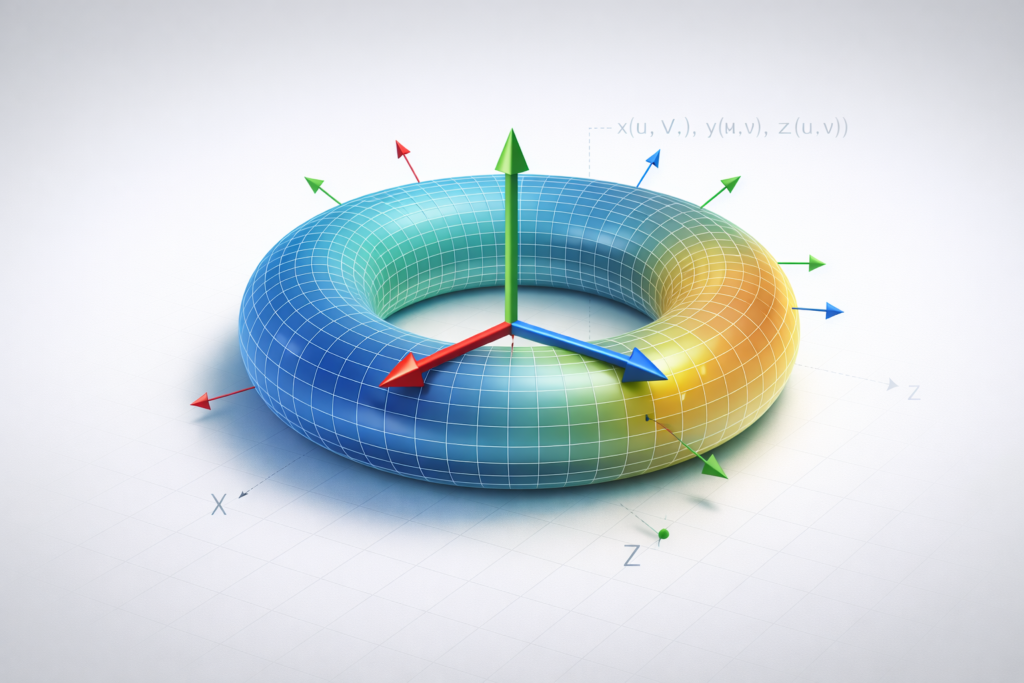
Whereas coordinate geometry is the description of the position of fixed points, dynamic curves and surfaces could be modelled by parametric equations. The point can be represented in parametric form, which is usually specified as a function of a parameter(s) commonly written ttt or (u,v)(u, v)(u,v).
Parametric Curves
It is possible to define a curve in 3D space as:
r(t) =(x(t),y(t),z(t))r(t) = (x(t), y(t), z(t))
Example: A circle in 2D:
x(t),y(t): rcos[?]t,rsin[?]t,0[?]t<2p x(t),y(t): rcos,rsin,0[?]: 0{?],0[?]: 0: rcos,rsin[?],xt,yt: rcos,rsin[?],xt,yt: rcos,rsin[?],xt,yt: rcos,rsin[?],xt,yt: rcos,rsin[?],xt,yt: rcos,rsin[?],
Computer aided design important Parametric curves are used in creating smooth paths and trajectories.
Parametric Surfaces
Often surfaces are given as functions of two variables:
S u v =(x(u,v),y(u,v),z(u,v))S uv= (x(u,v),y(u,v),z(u,v))
Example: A sphere:
x(u,v) = r sin u cos v, y(u,v) = r sin u sin v, z(u,v) = r cos u,xcosin[u] sininv[v]sininv[u]cosinv[v]sininv[v]cosinv[v]cosinv[v]cosinv[v]cosinv[v]cosinv[v]cosinv[v]cosinv[v]cosinv[v]cosinv[v]cosinv[v]cosinv[v]cosinv[v]cosinv[v]cosinv[v]
Complex organic shapes, including automotive bodies, anatomy models, and molecule structures, can be modeled with the help of parametric surfaces. They enable the strict regulation of the curvature and smoothness, which is important in the designing process, both aesthetic and practical.
Visualization Technology Theory and Visualization Technology Bridging
The above mathematical gifts, which include coordinate geometry, vector algebra, transformations, and parametric equations, are the workhorse of the geometrical modelling. They are not limited to theory but can be utilized in the visualization technologies.
Computer-Aided Design (CAD)
Mechanical components, architectural structures, and electronic devices are the things in which the principles of CAD software are worked into precise models. The stress analysis, fluid dynamics, and thermal behaviour can be simulated by engineers on the basis of mathematically accurate geometric representations.
Scientific Visualization
Parametric surfaces and vector-based transformations aid the visualization of complicated structures in other areas like molecule biology and geology. As an example, one may examine protein folding patterns or geology structure in detail with the assistance of research and education.
Animation and Gaming
Transformations and vector operations are vital in 3D graphics in animation and gaming. Motions of characters, turns of camera and rendering of scene are calculated mathematically making them consistent and realistic.
Interaction and Real-Time Manipulation
The mathematical foundations enable the user to deal with models in real-time. Dynamic transformations are implemented and with parametric definitions, continuous deformation and animation is possible. The ability is essential in the virtual simulation, training modules or the interactive design reviews.
Conclusion
Geometric modeling is an incredible combination of technology and mathematics. Through coordinate systems, the manipulation of vectors, transformations and, parametric equations, it makes complex shapes easy and flexible to manipulate and precisely represent. It does not only help increase the accuracy of design and simulation but also provides a connection between theoretical mathematics and the applied tools of visualization in modern science, engineering and digital media, and is therefore an indispensable science in modern-day science, engineering, and digital media.
Knowing these mathematical roots will enable practitioners to design models that are more complex, enable them to take their visualization capability to new heights, and enable them to make abstract ideas more lifelike and interactive.